Integrasjon Made Simple

I matematikk, er integrering beregning av et område definert av en funksjon. For å finne integralet av en funksjon er å finne området mellom funksjon og en base, for eksempel x-aksen. Integrering er av større betydning, men i å summere produkter av å endre variable og håndtering endrings generelt.

Området Under en kurve

De gamle grekerne hadde mange metoder for å finne området eller volumet av en figur. Integrasjon laget for en mer universell verktøyet. Integrasjon kan bli sett på som en summering av meget smale rektangler under en funksjon f (x). Hvis «x er bredden av hvert rektangel, da arealet av et rektangel på x er f (x) ganger" x, eller høyde ganger bredden. Slik at området fra for eksempel 0 opp til en er f (0) «x + f (« x) "x + f (2" x) "x + ... + f (1)" x.

Jo mindre vi sette "x, desto mer nøyaktig estimat av området. Notasjonen for denne integreringen er ∫f (x) dx. Den" blir d når bredden på rektanglene blir forsvinnende.

Forholdet til den antideriverte

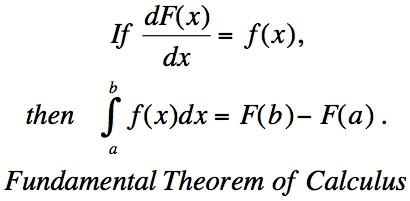
Integralet av en funksjon er knyttet til dens antideriverte. (En antideriverte, F (x), av en funksjon, f (x), har den egenskapen at f (x) er stigningstallet til f (x) for x.) Dette forholdet ble påvist geometrisk av Isaac Barrow, en av Isaac Newtons professorer ved Cambridge. Forholdet er at integralet av (areal under) f (x) mellom punktene a og b er lik F (b) -F (a). Dette forholdet er så viktig at den har det spesielle navnet analysens fundamentalteorem.

Å vite for eksempel at hellingen (dvs. et derivat eller en endringshastighet) til x-squared ved x er 2x, kan vi finne arealet under funksjonen 2x. Nærmere bestemt arealet under kurven 2x fra x = 0 til x = 1 er x-squared ved en minus x-squared på 0, dvs. 1 ^ 2 - 0, ^ 2 = 1.

Bruker

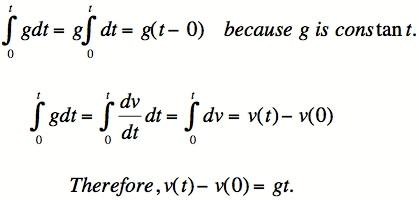
Smal rektangel måte å vise integraler kan være nyttig i besvare et spørsmål som hvordan å bestemme den totale arbeid utført av en kraft over en varierende bane. Integrasjonen vil være over kraft ganger "(avstand), hvor kraften er rektangulær høyde og" (avstand) er bredden. Et annet rektangel problem er å bestemme styrken på en dam, med press varierende med dybde. Integrasjonen vil være overtrykk ganger "dybde ganger" bredde.

En annen betydelig bruk av integrering er i sannsynlighet. Dersom arealet under en funksjon er 1, og området mellom x = a og x = b representerer sannsynligheten for at enkelte variable som mellom a og b, så integralet av funksjonen fra a til b gir verdien av denne sannsynlighet.

Rektangler side, integrering virkelig viser sine muskler når du arbeider med endrings. For eksempel, på overflaten av jorden, gravitasjons frekvensen av akselerasjon, g, er en konstant 9,80 meter per sekund-squared. Akselerasjon er frekvensen av endring av hastighet, så hastigheten er antiderative akselerasjon. Derfor kan hastigheten av et objekt med ingen andre krefter som på den bort fra tyngdekraften bli funnet etter tiden t ved integrasjon. Et annet integrasjons - denne tiden av v (t) som frekvensen av forandring av stilling - tillater beregning av den posisjon etter tiden t.

En overflod av metoder

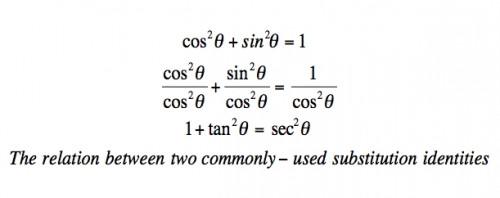
Hva forvirrer mange førstegangsstudenter kalkulus er hvor mange metoder det er å integrere: substitusjon, trigonometrisk substitusjon, delvis integrasjon, og delvis fraksjoner. Den beste strategien for å forenkle det er å innse at listen er kort, og en anmeldelse av hvilke former for ligninger vike for hva metode. Grunnleggende for raskt å identifisere hvilken metode å bruke er å raskt avgjøre om trig substitusjon er nyttig eller ikke. For å oppnå dette, hjelper det å huske de to relevante trigonometriske identiteter: cosinus-squared + sinus-squared = 1 og 1 pluss tangent-squared er sekant-squared. Det er lett å huske den sistnevnte ved å notere det er bare den tidligere dividert med cosinus-kvadrat. (For den saks skyld, cos-squared + synd-squared = 1 er lett å huske, fordi det er bare Pythagoras 'læresetning for en enhet sirkel.)