Spesielle Factoring Techniques

Polynomer er funksjoner av variabler med ulike eksponenter. Rekkefølgen av polynomet er det høyeste antall variable multiplikasjoner i en addend. For eksempel, rekkefølgen av xy + 1 er 2. Rekkefølgen av x ^ 3 + 1 er 3. polynomer orden 2 og 3 er kalt quadratics og cubics respektivt. Binomial ligningen, omvendt folie, og factoring ved å gruppere er alle velkjente facto teknikker. Noen spesielle teknikker, men er kraftigere, og kan faktor når disse vanlige teknikker ikke kan.

halverings~~POS=TRUNC

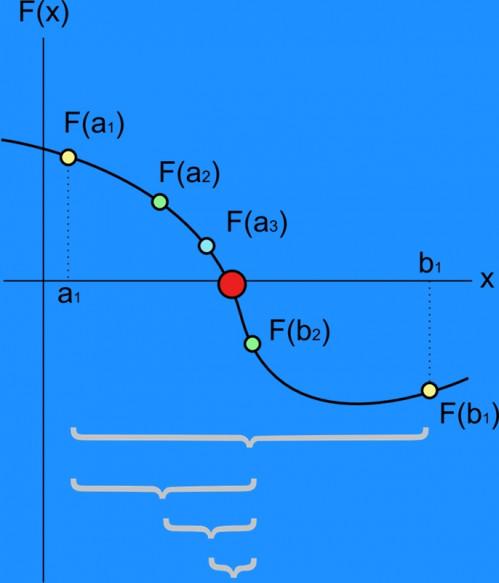
En numerisk (dvs. bruk av en datamaskin) tilnærming til factoring er å løse for nullpunktene til polynomet av konvergens. Anta polynomet er p (x). Målet er å finne x som løser p (x) = 0. Dette kan gjøres ved å starte ut med to nære estimater av x: x1 og x2. De bør være slik at p (x1) og p (x 2) er av motsatt fortegn. Så gjennomsnittet av x1 og x2 og kaller det x3. Løs for tegn på p (x3). Bruk x3 å erstatte x1 eller x2 som produserer det samme tegn i p (x). Den x3 vil være nærmere svaret, slik at x som er lenger unna blir forkastet. Midlingen blir gjentatt for å få x4, x5, etc., inntil algoritmen konvergerer på en enkelt x som produserer p (x) = 0. Denne x vil være en av røttene til p (x).

cubics

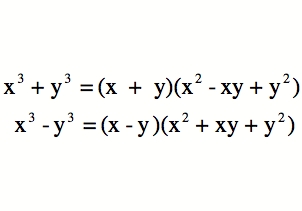
Forskjellen og summen av kuber har enkle factorizations, men cubics generelt kan løses, også, selv om faktorisering er ikke enkel. På grunn av sin kompleksitet, er det best å først se om du kan gjette en rot. I så fall kan du dele (x-root1) i kubikk for å produsere en kvadratisk.

Hvis ikke, algoritmen til bruk er en dobbel-substitusjon, først utgitt av Girolamo Cardano. Skjemaet til å begynne med er x ^ 3 + ax ^ 2 + bx + c = 0. Innbytter x = a / 3, der z er en variabel. Deretter omgruppere vilkår. (3b-en ^ 2) / 3 vil være koeffisienten til z. Definere p = (3b-a ^ 2) / 3, få erstatning z = wp / 3x (kalt Vieta er substitusjon). Deretter omgruppere. Formelen vil bli en kvadratisk i w ^ 3, som er lett løsbar ved hjelp av den kvadratiske ligningen.

Den Wolfram linken gir et bevis, som starter på linje 25.

skjulte Quadratics

Quadratics er av formen ax ^ 2 + bx + c. Røttene er selvfølgelig løsningen å øks ^ 2 + bx + c = 0. Løsningen kalles den kvadratiske ligningen, er tungt boret i algebra klasser --- ikke noe spesielt. Men noen ganger quadratics er skjult i en annen form, slik at det er ikke åpenbart at løsningen er en ren anvendelse av kvadratisk likning. Eksempler er: x ^ 4-3x ^ 2 + 4 = 0; (X + 2) / (x ^ 2 + 1) = 4; exp (x) -exp (-x) = 8; og [x-1 / x] / 2 = 4. (Exp (x) selvfølgelig refererer til eksponenter av argumentet med undersiden av den naturlige logaritmen som base av eksponenten, dvs. exp (x) = e ^ (x)).

Løsningen på disse eksemplene er enten å bruke substitusjon eller til å formere gjennom for å fremstille den kvadrerte sikt. For eksempel, i første eksempel erstatte x ^ 2 med u. I den andre, multiplisere gjennom av nevneren. I den tredje, multiplisere gjennom av exp (x). I den fjerde, multiplisere gjennom av x.